LTS: Tòa soạn đã nhận được bài viết thể hiện quan điểm của Giáo sư Nguyễn Tiến Dũng, thực hiện theo đề nghị của thầy Ngô Văn Minh (Giáo viên toán Trung học Cơ sở Archimedes) bàn về cách nâng cao chất lượng giảng dạy môn hình học tại Việt Nam.
Giáo sư Nguyễn Tiến Dũng là một nhà toán học người Việt tại thành phố Toulouse (Cộng hòa Pháp), được phong Giáo sư vào năm 2002 khi 32 tuổi, và được phong thành Giáo sư ngoại hạng (classe exceptionnelle) vào năm 2015.
Ông từng đạt Huy chương Vàng Olympic Toán quốc tế (IMO) năm 1985 tại Phần Lan khi mới 14 tuổi, và là học sinh đạt Huy chương Vàng IMO trẻ nhất của Việt Nam từ trước tới nay.
Tòa soạn trân trọng gửi đến độc giả bài viết!Các học sinh đi thi toán quốc tế IMO của Việt Nam thường mạnh về hình học sơ cấp mà yếu về toán tổ hợp so với các nước khác.
Lý do là toán tổ hợp đòi hỏi suy nghĩ sáng tạo, còn các bài toán hình học sơ cấp thường chỉ cần được luyện nhiều là làm được, hợp với kiểu học và luyện thi hiện tại của Việt Nam.
Nhưng đó là nói về học sinh thi toán quốc tế, còn đối với rất nhiều học sinh khác, thì môn hình học lại là một môn khó, đáng sợ hơn môn đại số. Thậm chí có những học sinh thuộc diện thủ khoa đầu vào Trung học Cơ sở các trường TOP như Hanoi Amsterdam cũng cảm thấy thiếu tự tin khi gặp các bài toán hình học. Vì sao vậy?
Theo thầy Nguyễn Khắc Minh (chuyên gia của Bộ Giáo dục và Đào tạo), một lý do chính là cách dạy hiện nay.
Đi vào phân tích kỹ hơn, chúng ta có thể nhận thấy một số nhược điểm trong cách dạy môn hình học phổ biến hiện nay như sau:
1) Không tạo được cảm hứng cho học trò.
2) Thiếu cơ bản, dập khuôn giải các dạng bài thay vì chú trọng đến việc hiểu cốt lõi vấn đề.
3) Cô lập, không chỉ ra các ứng dụng và sự liên quan đến những thứ khác.
4) Quá hình thức, không kích thích phát triển khả năng hình dung hình học.
Tôi xin đưa ra đây một số chi tiết và ví dụ minh họa, cũng là để bàn về việc nên thay đổi cách dạy (và cách học) như thế nào cho hấp dẫn và hiệu quả hơn.
Trước hết, về Điểm 4:
Tất nhiên, cả 4 điểm trên đều có thể nói cho việc dạy mọi môn khác chứ không riêng hình học. Điểm đặc biệt của hình học nằm ở chỗ nó không những sử dụng suy luận logic mà còn đòi hỏi cao và phát triển mạnh khả năng hình dung hình học trực giác (Tư duy hình dung trực giác ở các môn khác cũng cần, nhưng đặc biệt trong hình học nó càng thể hiện rõ).
Nói về thần kinh học, thì tức là nó dùng cả não trái (tính toán logic) và não phải (trực giác hình học).
Tương tự như là trong máy tính và smartphone có cả “main processor” và “graphics processor” vậy, cả hai đều quan trọng để cho nó chạy nhanh chạy tốt. Nếu không vận dụng phần não phải thì tư duy hình học ắt bị ảnh hưởng nhiều.
Một lần tình cờ tôi xem trên youtube một bài giảng kéo dài khoảng một tiếng của một giáo viên Việt Nam về phép quay. Chỉ cần nghe một số phút đầu tiên tôi đã xác định thấy đây là một bài giảng chán, khiến học sinh sợ môn hình.
Ngay mở đầu bài giảng, giáo viên đã nói: “Phép quay là một vấn đề khó”.
Tiếp đó, giáo viên đưa ra định nghĩa phép quay một cách hình thức, kiểu như:
“Phép quay là một phép biến đổi trong mặt phẳng sao cho nó cố định một điểm A và nó biến mỗi điểm P thành một điểm P’ thỏa mãn những điều kiện sau: …” (trong lúc giáo viên nói định nghĩa đó, thì cũng không hề chỉ vào một hình nào để minh họa, mà chỉ nói như tụng kinh).
Định nghĩa này không sai, chỉ có điều nó không trực giác, khó theo dõi (nhớ được đủ các ký hiệu đã đủ mệt, chưa nói đến chuyện hiểu), và không thích hợp để làm điểm khởi đầu cho một bài giảng về phép quay.
Thay vào đó, có thể giảng như thế nào cho sinh động, dễ hiểu? Tôi xin đưa ra vài gợi ý:
- Đừng bao giờ nói “Cái này khó lắm”. Mọi khái niệm toán học ở phổ thông đều trong sáng, tự nhiên, chẳng có cái gì “khó lắm”.
Khó thì không phải là do bản thân kiến thức khó, mà cách tiếp cận không thích hợp biến cái dễ thành cái khó (và biến cái khó hơn thành cái không thể hiểu, xin trích ra đây một câu chuyện có thật: bản thân nhiều giảng viên Đại học không hiểu bản chất cái mình giảng).
- Phép quay là phép biến đổi rất tự nhiên mà học sinh trước khi đi học đã nhìn thấy tận mắt hàng ngày. Cần bắt đầu bởi những cái mà học sinh đã biết đó: bánh xe đạp quay, kim đồng hồ quay, cối xay quay…
Những cái đó có “khó” không? Sao không cầm một cái gì đó cắm vào một trục và quay nó trước mặt học sinh? Sẽ thật dễ hiểu và trực giác. Sẽ thấy ngay trục quay là điểm cố định, các điểm khác dời chuyển đi vì thỏa mãn các tính chất dễ thấy bằng trực giác.
Rồi sau đó mới đến đoạn kiểm tra các tính chất đó một cách chặt chẽ, viết thành định lý. Chú ý là chứng minh của một định lý dù có đúng cũng chưa chắc đã là cách giải thích hay ho cho học sinh hiểu.
Đầu tiên cần hiểu ý tưởng vì sao nó lại đúng, rồi mới đến chứng minh chặt chẽ, mới là quá trình tiếp cận hiệu quả hơn.
- Đưa ra một số ví dụ về việc phép quay cho phép chúng ta tìm ra lời giải đẹp đẽ nhanh gọn cho nhiều vấn đề như thế nào. Những ví dụ đó sẽ giúp học sinh thấy khái niệm này bổ ích, đáng nhớ, đáng học.
Chẳng hạn như ví dụ sau (xem hình đính kèm):
 |
| Ví dụ. |
Cách giải bài trên theo lối “thông thường” mà học sinh Việt Nam được học sẽ thông qua việc chứng minh các tam giác bằng nhau (ví dụ tam giác OAP bằng tam giác ODQ theo tiêu chuẩn c-g-c) và gồm nhiều bước. Nhưng nếu quan sát sẽ thấy ở đây ta có phép quay 90 độ quanh O, và nó phải biến điểm Q thành điểm P.
Lời giải theo phép quay này là lời giải tự nhiên nhất và gọn gàng nhất: Phép quay 90 độ quanh O theo chiều dương biến D vào A, biến A vào B. Do đó nó biến đường thằng DQ vào đường thẳng AE (vì hai đường này tạo với nhau một góc 90 độ bằng với góc quay), biến đường thẳng AE vào đường thẳng BP (với lý do tương tự), do đó nó biến giao điểm của hai đường DQ và AE (tức là điểm Q) vào giao diểm của hai đường AE và BP (tức là điểm P).
Suy ra OQ quay thành OP theo phép quay 90 độ, tức là OQ = OP và góc QOP bằng 90 độ.
Bài tập trên lấy từ một quyển sách rất hay về hình học sơ cấp nhan đề “Xung quanh phép quay – Hướng dẫn môn hình học sơ cấp”, được Giáo sư Nguyễn Hùng Sơn và Giáo sư Nguyễn Sinh Hoa (Đại học Tổng hợp Warszawa, Ba Lan) giới thiệu và dịch ra tiếng Việt.
Tác giả của nó là Giáo sư Waldemar Pompe (cũng của Đại học Tổng hợp Warszawa), người phụ trách đội tuyển IMO của Ba Lan trong nhiều năm. Tuy gọi là “phép quay” nhưng thực ra sách giới thiệu công dụng của các phép dời hình nói chung (cả quay, tịnh tiến và đối xứng gương) trong hình học phẳng.
Như Pompe có viết, hầu hết các định lý hình học sơ cấp suy ra được từ hai quan sát cơ bản: quan sát thứ nhất là bất đẳng thức tam giác, và quan sát thứ hai là các phép dời hình vừa kể trên là các phép bảo toàn các số đo hình học.
Các tiếp cận hình học này vừa tự nhiên vừa hiện đại, và cho phép hiểu và giải quyết một cách đẹp đẽ nhiều vấn đề hình học khác nhau, ví dụ như bài toán tối ưu sau (gọi là bài toán Fermat): Có ba cái nhà (3 đỉnh của tam giác) trên mặt phẳng. Hãy tìm đường ngắn nhất nối 3 cái nhà đó với nhau.
Có vị ở Việt Nam phô trương là dạy được toán cao cấp như là lý thuyết nhóm cho học sinh cấp 1 bằng “công nghệ giáo dục” của mình. “
Công nghệ” dạy đó như thế nào? Hoàn toàn hình thức. Đưa ra định nghĩa hình thức về nhóm (như là có thể tìm thấy trong các sách về đại số cao cấp), rồi đưa ra mấy ví dụ hình thức bắt học trò kiểm tra nó thỏa mãn cái định nghĩa trên để kết luận đó là nhóm.
Cách dạy đó là cách dạy vô nghĩa, không làm cho học sinh hiểu bản chất vấn đề, không biết nhóm dùng để làm gì, tại sao lại phải học nó.
Trong khi đó, các phép dịch chuyển trong hình học chính là các phần tử của các nhóm đối xứng, và việc quan sát tác động của chúng, sử dụng các tính chất của chúng để giải quyết các vấn đề mới làm cho chúng trở nên có nghĩa, sinh động.
Về Điểm 3:
Trong khuôn khổ có hạn của sách giáo khoa hiện tại, có thể không có nhiều chỗ cho việc giới thiệu các ứng dụng và xuất phát điểm của các khái niệm hình học.
Nhưng nếu vậy thì cần thêm sách tham khảo cho học sinh đọc để biết nhiều thêm về ứng dụng thực tế của hình học ra sao, và giáo viên nên nhắc đến chúng khi giảng bài chứ không sẽ thành “lý thuyết suông”.
Một bạn kể rằng, khi học phổ thông học hình học chẳng hiểu gì cả, nhưng khi vào đại học phải học môn đồ họa, tự nhiên thấy hình học dễ hiểu hẳn. Tại sao lại không nhắc đến hình họa trong hình học?
Không chỉ hình hoạ, mà rất nhiều vấn đề “thường ngày” khác cần đến kiến thức hình học sơ cấp.
Chẳng hạn như xây tường để khỏi đổ thì tường phải đứng thẳng, tức là vuông góc với mặt đất. Mặt bàn thì phải đặt nằm ngang, tức là song song với mặt đất nếu không muốn các thứ đặt trên đó bị lăn trượt đi, bánh xe đạp thì phải tròn thì mới lăn tốt mà xe không bị nhấp nhô…
 |
Gần đây tôi có viết một quyển sách nhan đề “Toán học và Nghệ thuật”, trong đó có nhiều ví dụ thực tế về việc hình học ảnh hưởng trực tiếp đến các nghệ thuật tạo hình và kiến trúc ra sao. Đây là sách viết về toán nhưng cho những người không cần có kiến thức chuẩn bị gì về toán, và mục đích chính là để gây cảm hứng, cho thấy toán học có ý nghĩa ra sao (trong nghệ thuật).
Hy vọng bạn đọc sẽ thích nó, đặc biệt nếu đang sợ hình học!
(“Nghịch lý cột đền” về chuyện cột ở giữa trông có vẻ nhỏ hơn các cột bên cạnh tuy thực ra chúng bằng nhau, và ảo giác về zombi to nhỏ khác nhau, là hai trong số nhiều ví dụ về hình học sơ cấp được giải thích trong sách “Toán học và nghệ thuật”).
Chẳng hạn như môn “hình học xạ ảnh” nảy sinh chính từ việc vẽ phối cảnh hình sao cho trông giống như thật.
Từ “xạ ảnh” gốc Hán Việt nghe kỳ bí, khó hiểu, tuy thực tế không đến mức khó hiểu như vậy. Tiếng Tây của từ này là “projective”, có nghĩa là phép chiếu, tức là hình học của các phép chiếu.
Khi vẽ hình một đồ vật hay phong cảnh (3 chiều) nào đó, là ta đã chiếu nó lên tờ giấy hay khung tranh 2 chiều.
Chính vì thế muốn vẽ đẹp, vẽ đúng, cần biết một số nguyên tắc cơ bản của hình học phép chiếu (tức là hình học xạ ảnh). Ở trường phổ thông cũng có môn học vẽ, nhưng có lẽ thầy giáo vẽ chẳng bao giờ đả động đến kiến thức phép chiếu của hình học, còn thầy hình học chẳng đả động đến điêu khắc, hội họa hay vẽ kỹ thuật.
Tạo được sự tương tác thì học sinh sẽ học tốt hơn, hiểu rõ hơn cả hình học lẫn các môn kia.
Về Điểm 2:
Cách học “ăn sổi”, “mì ăn liền”, chạy theo điểm số ở Việt Nam là một trong những lý do khiến học sinh học hời hợt, có thể giải bài tập (những dạng bài được làm đi làm lại nhiều lần, hoặc có trong quyển sách luyện thi nào đó) như cái máy mà không hiểu bản chất vấn đề. Điều này thực sự đáng ngại, và càng học lên cao và khi ra ngoài làm việc càng lộ rõ.
Có những khi tôi phỏng vấn những sinh viên cao học ngành toán thuộc loại xuất sắc của Việt Nam (cho việc du học tại Pháp), sinh viên kể đã học những môn “rất cao cấp”, nhưng khi hỏi một số câu hỏi khá cơ bản (cao cấp vừa phải thôi) thì không trả lời được, chứng tỏ học vội vàng và hổng nhiều.
Trong môn hình học ở bậc phổ thông, tình trạng có lẽ cũng tương tự như vậy, chạy theo điểm số hình thức mà bỏ qua bản chất của kiến thức.
Tôi thử lấy một bài tập ví dụ, nếu học sinh hay thầy cô nào quan tâm thí nghiệm thử xem sao:
- Hãy tự chứng minh các tính chất đồng quy của các bộ ba đường cao, ba đường trung tuyến, ba đường trung trực, và ba đường phân giác.
- Tại sao nếu biết 3 cạnh của một hình tam giác thì xác định được diện tích của nó?
Tất nhiên, những câu hỏi trên có tính lý thuyết và đã đều có phát biểu và chứng minh trong sách.
Nhưng hãy thử không học thuộc lòng chứng minh của sách, tự mình khôi phục lại cách chứng minh bằng lập luận của mình, thì có làm được không? Hay lấy những bài tập đơn giản kiểu như:
- Có ba đoạn thẳng với độ dài tương ứng là 3, 4, 6 (cm). Dựng tam giác với độ dài các cạnh như vậy, nó là tam giác nhọn, hay vuông, hay tù? Vì sao? Tính diện tích của nó?
Nếu học sinh nào làm được, tức là hiểu đáng kể hình học phẳng, đừng quá bận tâm nếu không làm được các bài hình học rắm rối.
Chúng sẽ trở nên dễ dàng hơn một khi ta hiểu bản chất các khái niệm hình học, và học một vài phương pháp thông dụng để giải bải tập (ví dụ như phương pháp sử dụng phép đối xứng như bàn đến ở trên, phương pháp vẽ thêm đường phụ, và phương pháp quỹ tích).
Một trong những cuốn sách giáo khoa trình bày hình học sơ cấp một cách cơ bản, sáng sủa nhất mà tôi biết là cuốn “Hình học sơ cấp” của Kiselev (gồm hai phần, “Hình học phẳng” và “Hình học không gian”).
Các bài tập trong sách đó (mà sách có rất nhiều bài tập) chủ yếu là ở dạng cơ bản, không rắm rối, làm được là hiểu được bản chất hình học.
Thầy giáo Tôn Thân nổi tiếng khi xem sách Kiselev cũng trầm trồ khen đây là quyển sách rất hay.
Các bài mẹo mực dở ở chỗ nó làm lệch lạc nhận thức về việc đâu là kiến thức cơ bản quan trọng: học sinh dễ bị sa đà vào cái mẹo mực ít ý nghĩa thay vì cái cơ bản hữu dụng, và khi không làm được cái mẹo mực lại đâm thành sợ toán, ghét toán.
Các bài kiểm tra học sinh không nên quá rối rắm hay đòi hỏi nhiều mẹo mực.
 |
| Một hình minh họa từ sách “Hình học sơ cấp” của Kiselev, một quyển sách rất cơ bản, không mẹo mực, và chứa rất nhiều kiến thức hay mà học sinh Việt Nam không được học. |
Về điểm 1:
Các điểm 2, 3, 4 kể trên chính là những điểm góp phần làm học sinh mất hứng thú với hình học, tạo lại được cảm hứng cho học sinh là điều quan trọng, vì một khi có cảm hứng thì học sẽ nhanh vào.
Trong điều kiện mà cảm hứng tạo ra được trong giờ học chính thức có hạn, thì học sinh nên tìm hiểu thêm các hoạt động ngoại khóa sinh động, và đọc các sách tham khảo hấp dẫn.
Ở Việt Nam từ trước đến nay cũng đã có các quyển sách tham khảo thú vị, có tác dụng gợi mở cảm hứng, về toán học nói chung và hình học nói riêng.
Ví dụ như là quyển “Hình học vui” của Perelman, hay quyển “Thuyền trưởng đơn vị” của Levshin (Cả hai đều được dịch từ tiếng Nga, và người ta có thể chê nước Nga về thứ này thứ khác nhưng không thể phủ nhận là Nga có thời kỳ hoàng kim về toán và vật lý, phóng vệ tinh “Sputnik” vào vũ trụ trước Mỹ).
Tuy nhiên, theo tôi được biết, nếu như các sách giáo khoa dù hay dở ra sao cũng được in với số lượng hàng trăm nghìn bản mỗi lần, thì các sách tham khảo hay được phát hành với số lượng còn rất khiêm tốn (chỉ vài nghìn bản).
Trên thị trường sách tham khảo thì vẫn chủ yếu là các sách bài tập, luyện thi “mì ăn liền” chiếm ưu thế áp đảo, chứ lượng sách tham khảo có tính gợi mở, khơi dậy cảm hứng còn rất ít, trung bình có lẽ cứ hàng trăm học sinh thì mới có được một học sinh có sách như vậy, mà sách như vậy mới dễ đem lại cảm hứng cho học sinh.
Hy vọng tình hình sẽ thay đổi trong tương lai gần, tất nhiên học sinh có nhu cầu điểm cao để còn được vào trường tốt, nhưng kiểu học chỉ hướng tới điểm thi mà không có cảm hứng hay hiểu bản chất là kiểu học kém hiệu quả về lâu về dài.
Nếu muốn chuyển từ ghét hình học, sợ hình học sang thành thích hình học, thì đặc biệt cần những sách khác nữa, ví dụ như là những quyển sau:
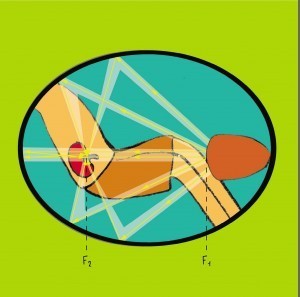 |
| Một tranh trong sách “Một ngày phiêu lưu trong thế giới toán học kỳ diệu” về ứng dụng hình học vào việc chữa sỏi thận. |
-“Thuyền trưởng đơn vị” của Levshin: Câu chuyện du hành ly kỳ của chú bé Số Không, qua đó có những giải thích sinh động về điểm, đường, tiên đề, định lý, trọng tâm, các đường đặc biệt trong tam giác…
- “Một ngày phiêu lưu trong thế giới toán học kỳ diệu” của Akiyama và Ruiz: Có nói đến nhiều loại đường và mặt khác nhau xuất hiện trong thực tế ra sao, ví dụ như mặt của ăng ten parabol, mặt ellipsoid dùng trong máy chữa sỏi thận, các hình có độ rộng không đổi mà không nhất thiết phải tròn…
Ngô Văn Minh
Tên bài gốc "Làm theo các cách sau, môn hình học sẽ không còn là nỗi ám ảnh nữa"



0 nhận xét:
Đăng nhận xét